Comprendiendo las Decisiones Cruciales: Aplicación Práctica de Regresión Logística en Aprendizaje Supervisado

Introducción:

En el vasto espectro del aprendizaje supervisado, la Regresión Logística destaca como una herramienta esencial para la clasificación. Este algoritmo, a pesar de su nombre, no está destinado a problemas de regresión, sino que se utiliza para abordar problemas de clasificación binaria. En esta entrada, exploraremos los conceptos clave de la Regresión Logística, lo implementaremos en un caso de estudio relevante, y analizaremos cómo interpretar los resultados.

Contextualización:

A medida que la necesidad de tomar decisiones basadas en datos se vuelve cada vez más crítica, la Regresión Logística ha emergido como una herramienta confiable para la clasificación en campos que van desde la medicina hasta la ingeniería. Su capacidad para prever resultados binarios la convierte en un pilar indispensable en la caja de herramientas del aprendizaje supervisado.

Desarrollo:

Conceptos Clave de la Regresión Logística:

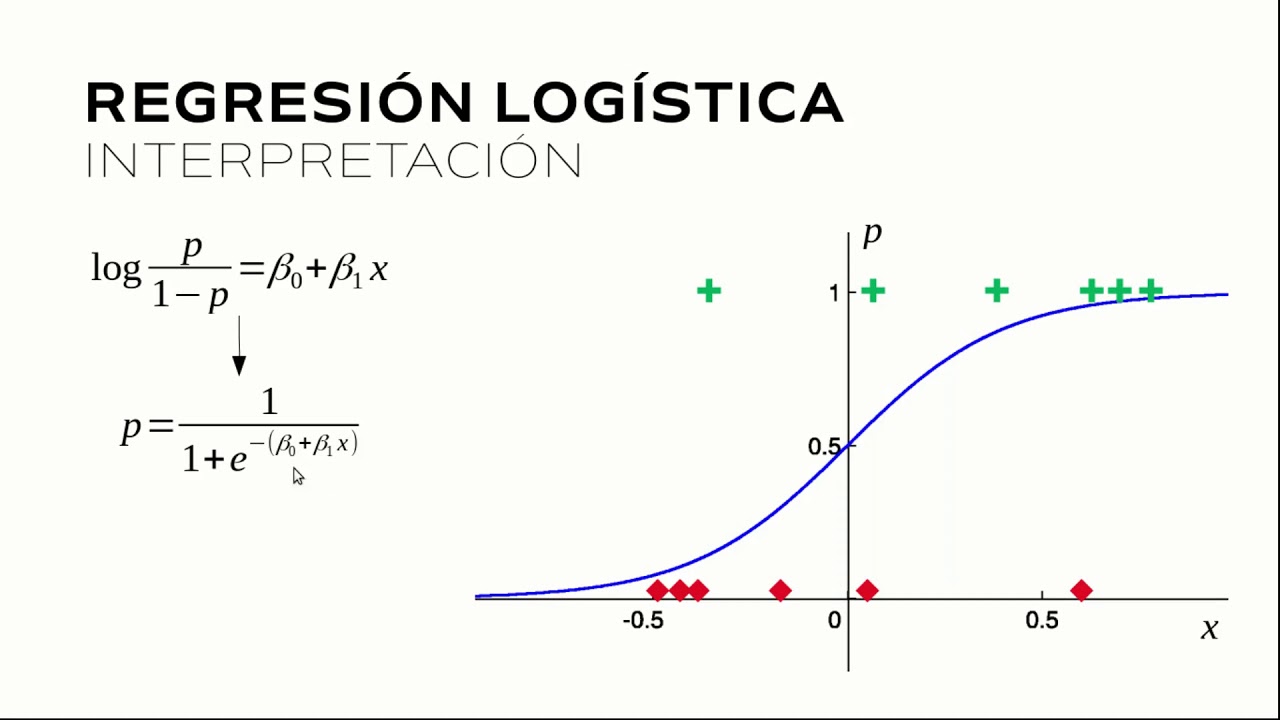
A diferencia de la regresión lineal, la Regresión Logística se utiliza para problemas de clasificación binaria. La función sigmoide transforma la salida en un rango entre 0 y 1, interpretado como la probabilidad de pertenecer a una clase.

Implementación en un Caso de Estudio:

Imaginemos que queremos predecir si un pozo de petróleo es productivo o no en función de ciertos indicadores. Utilizaremos datos ficticios para entrenar y evaluar nuestro modelo.

        # Código para la carga de datos y visualización         import pandas as pd         import numpy as np         import matplotlib.pyplot as plt         from sklearn.model_selection import train_test_split         from sklearn.linear_model import LogisticRegression         from sklearn.metrics import confusion_matrix, classification_report         # Generación de datos ficticios         np.random.seed(42)         features = np.random.rand(100, 2) * 10 # Características del pozo         labels = np.random.choice([0, 1], size=100) # Etiqueta binaria: 0 o 1         data = pd.DataFrame({'Feature1': features[:, 0], 'Feature2': features[:, 1], 'Label': labels})         # Visualización de la relación entre características y etiquetas         plt.scatter(data['Feature1'], data['Feature2'], c=data['Label'], cmap='viridis')         plt.title('Relación entre Características y Productividad del Pozo')         plt.xlabel('Feature1')         plt.ylabel('Feature2')         plt.show()

        # Código para la aplicación de la Regresión Logística         X = data[['Feature1', 'Feature2']]         y = data['Label']         # División del conjunto de datos        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)         # Entrenamiento del modelo         model = LogisticRegression()         model.fit(X_train, y_train)         # Predicciones         y_pred = model.predict(X_test)         # Evaluación del modelo         conf_matrix = confusion_matrix(y_test, y_pred)         class_report = classification_report(y_test, y_pred)         print(f'Matriz de Confusión:\n{conf_matrix}\n')         print(f'Reporte de Clasificación:\n{class_report}')

Este código simula la clasificación de pozos de petróleo en función de características específicas utilizando la Regresión Logística.

Perspectivas y Tendencias:

A medida que los conjuntos de datos crecen en complejidad, la Regresión Logística se combina con técnicas avanzadas como la regularización para mejorar la capacidad predictiva y generalización del modelo.

Conclusiones:

1. La Regresión Logística es esencial para problemas de clasificación binaria.
2. La interpretación de coeficientes y la función sigmoide son clave para entender las predicciones.
3. La evaluación del modelo mediante métricas como la matriz de confusión y el informe de clasificación es fundamental.

Reflexiones:

¿Cómo podrías aplicar la Regresión Logística en tu campo de estudio o trabajo? Reflexiona sobre la importancia de tomar decisiones informadas basadas en la probabilidad y la clasificación.

En esta entrada, hemos explorado la aplicación práctica de la Regresión Logística en el contexto del aprendizaje supervisado, demostrando su utilidad en problemas de clasificación binaria.

¡Experimenta con tus propios conjuntos de datos y descubre el potencial de esta técnica en tu área de interés!